원뿔 부피 공식 소개
수학에서 원뿔은 밑면이 원이고, 하나의 꼭짓점으로 이어진 입체 도형입니다.
이 형태는 우리 주변에서 교각, 원뿔형 텐트, 아이스크림 콘 등 다양한 곳에서 쉽게 찾아볼 수 있습니다.
평소에 원뿔의 모습을 자주 접하다 보면, 이 도형의 부피를 알아야 할 필요가 생기는 경우가 종종 있습니다.
이때 필요한 것이 바로 원뿔의 부피 공식입니다.
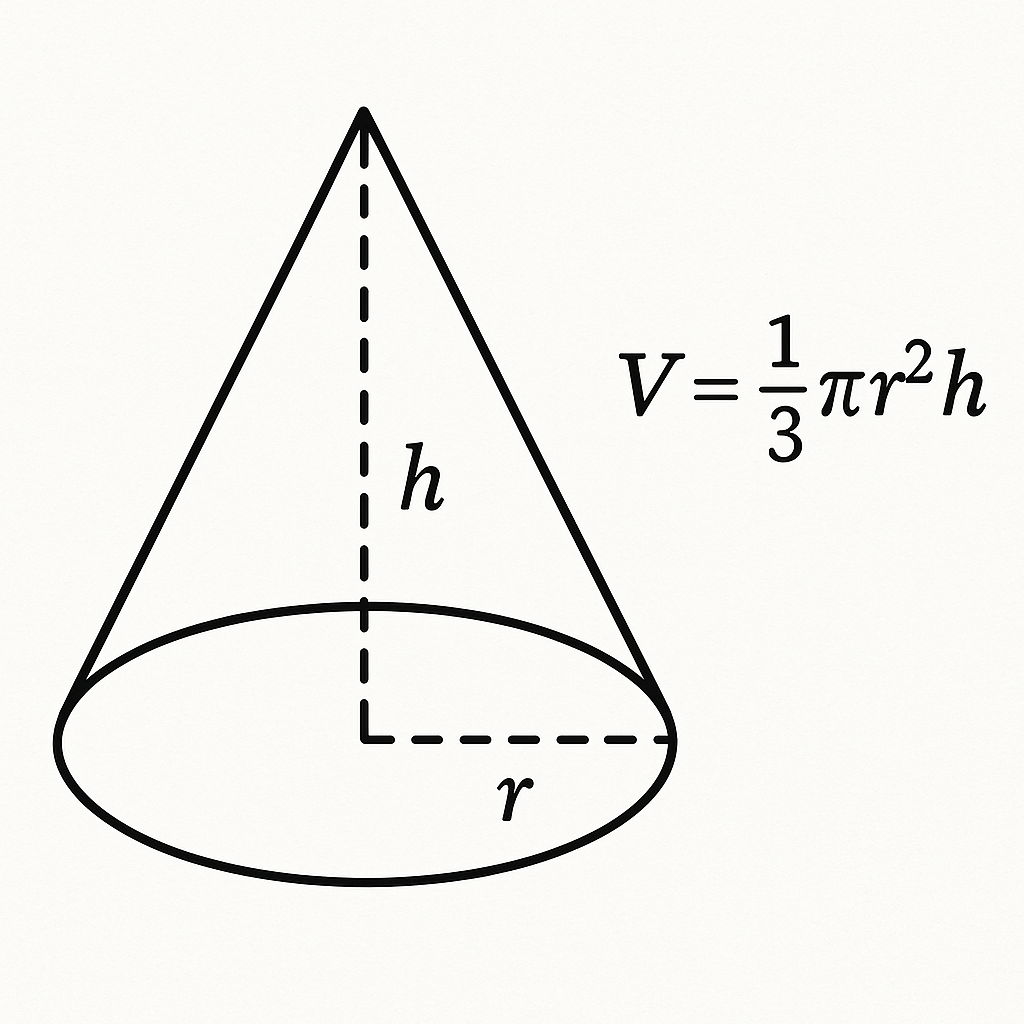
공식은 (1/3) × π × r² × h로 정리할 수 있습니다.
여기서 r은 밑면 원의 반지름, h는 원뿔의 높이, π는 원주율을 의미합니다.
이처럼 원뿔의 부피를 계산할 때 필요한 요소는 단 두 가지, 반지름과 높이뿐입니다.
공식을 바탕으로 실제로 계산해 보면,
예를 들어 반지름이 4cm, 높이가 9cm인 원뿔이 있다면,
부피는 (1/3) × 3.14159 × 4² × 9 ≈ 150.796cm³이 됩니다.
이렇게 간단한 곱셈과 나눗셈으로 원뿔 안에 들어갈 수 있는 양을 정확히 알 수 있습니다.
공식만 외우는 것이 아니라, 실제로 값을 대입하여 계산하는 연습을 반복하면,
각 요소가 최종 부피에 어떤 영향을 미치는지 직관적으로 느낄 수 있습니다.
원뿔 부피 공식의 특징
원뿔 부피 공식은 원기둥 부피 공식과 직접적인 관계가 있습니다.
원기둥의 부피 공식은 π × r² × h인데,
원뿔은 여기서 1/3을 곱해 구할 수 있습니다.
즉, 같은 반지름, 같은 높이의 원기둥과 원뿔이 있다면,
원뿔의 부피가 원기둥의 부피보다 정확히 3분의 1이라는 사실을 알 수 있습니다.
이 사실을 실제 실험으로 확인할 수도 있습니다.
만약 원뿔 모양의 용기에 물을 가득 채운 뒤,
그 물을 같은 크기의 원기둥 모양 용기에 부으면,
정확히 세 번을 옮겨야 원기둥이 가득 찹니다.
이처럼 공식은 이론적으로 증명되었을 뿐만 아니라,
실제 현상과도 완벽히 일치합니다.
이러한 관계성을 알면, 공식을 외우는 것보다 논리적으로 받아들이기 쉬워집니다.
또한, 원뿔과 원기둥, 구 등 다양한 도형의 부피 관계를 비교할 수 있게 되어,
넓은 시야에서 수학을 바라볼 수 있는 기회가 됩니다.
원뿔 부피 공식의 유래
원뿔 부피 공식의 유래는 고대 그리스 수학에서 찾아볼 수 있습니다.
수학의 아버지로 불리는 유클리드는 자신의 저서 〈원론〉에서
원뿔, 피라미드, 원기둥 등 다양한 입체도형의 부피에 대해 체계적으로 설명했습니다.
또한, 아르키메데스는 실험과 논리를 결합해 도형의 부피와 면적 공식을 여러 가지 증명했습니다.
특히, 아르키메데스는 실제로 모양을 잘라 붙이고,
비슷한 도형끼리 부피를 비교하는 방식으로 공식을 유도했습니다.
원뿔 부피 공식이 처음 등장한 이래,
수많은 수학자들이 다양한 방법으로 이를 증명하고,
현대에 이르기까지 여러 분야에서 널리 활용되고 있습니다.
이 공식은 이론상 증명된 내용이지만,
실제 실험을 통해 그 신뢰도를 확인할 수 있다는 점이 특징입니다.
과거의 수학자들이 남긴 지식에서 출발해,
오늘날 다양한 실생활에 응용되는 흐름을 느낄 수 있습니다.
원뿔 부피 공식 활용 예시
원뿔 부피 공식은 실생활의 매우 다양한 상황에서 유용하게 쓰입니다.
예를 들어, 건설 현장에서 원뿔형 구조물을 만들 때,
필요한 콘크리트나 철근의 양을 계산하는 데 활용할 수 있습니다.
제과점에서 원뿔형 케이크나 아이스크림 콘을 실제 크기로 만들 때,
반죽과 크림의 양을 정확히 파악하는 데도 이 공식이 필요합니다.
또한, 환경 분야에서는 원뿔형 부유물이나 보관 탱크의 부피를 측정할 때,
이 공식을 쓸 수 있습니다.
예를 들어, 반지름 5m, 높이 10m의 원뿔형 탱크에 담을 수 있는 물의 부피는
(1/3) × 3.14159 × 5² × 10 ≈ 261.799m³입니다.
이 값을 이용하면, 건물 내 물 저장조나 농업용 저수지 등
필요한 물의 양을 정확히 관리할 수 있을 것입니다.
학교 수업이나 시험에서도 원뿔의 부피를 묻는 문제가 자주 나옵니다.
반지름과 높이를 변형해서 여러 도형의 부피를 구하거나,
실생활에 적용하는 응용 문제를 풀 때,
이 공식만 정확히 기억하면 비교적 쉽게 답을 찾을 수 있습니다.
원뿔 부피 공식의 변형 및 응용
원뿔 부피 공식은 기본적으로 밑면이 원인 도형에 적용됩니다.
하지만 밑면의 모양이 타원이거나,
부분 원뿔(절단 원뿔, frustum)이라면 공식이 달라질 수 있습니다.
이럴 때는 전체 원뿔의 부피에서 잘린 부분의 부피를 빼거나,
적분을 통해 더 넓은 범위의 도형 부피를 구할 수 있습니다.
학교에서 배우는 기초 공식은 완전한 원뿔을 기준으로 하지만,
더 다양한 도형을 접하면서
변형 공식이나 응용 방법을 익히게 되면
수학적 시야가 확장될 수 있습니다.
특히, 고등학교 수준 이상에서는
적분을 통해 원뿔 부피 공식을 직접 유도하는 과정을 배우기도 합니다.
이 과정을 거치면,
단순히 공식을 외우는 것이 아니라
이유와 원리를 깨달을 수 있습니다.
원뿔 부피 공식 학습 팁
원뿔 부피 공식을 효과적으로 익히려면,
공식 자체를 외우는 것 외에도
실제로 손으로 계산을 해보는 것이 도움이 됩니다.
어떤 도형이든 반지름과 높이를 재고,
공식에 대입해 값을 구하는 연습을 반복하면
자연스럽게 공식이 기억에 남습니다.
여러 개의 원뿔이 있을 때,
각각의 부피를 따로 구한 뒤,
모두 더해 전체 부피를 구하는 방법도 시도해 볼 수 있습니다.
또한, 원뿔과 원기둥, 구 등 여러 도형의 부피를 비교해 보면,
각 도형의 특징과 관계를 한눈에 볼 수 있습니다.
학교에서 배우는 기본 공식은 매우 간단하지만,
실제 응용 문제나 고난도 수학에서는
추가적인 조건이나 다양한 변형이 등장하기도 합니다.
이 때, 기초 공식을 정확히 알고 있어야
변형된 문제도 풀어낼 수 있습니다.
실생활에서의 원뿔 부피 활용
원뿔 부피 공식은 일상에서 접할 수 있는 다양한 사물에 적용할 수 있습니다.
예를 들어, 파티용 천 조각을 원뿔 모양으로 접었을 때,
내부에 얼마나 많은 사탕이나 간식이 들어가는지 궁금하면
반지름과 높이를 재고, 공식에 대입해 볼 수 있습니다.
또한, DIY로 집 앞 마당을 꾸미기 위해
작은 종이뿔을 여러 개 만들어 쌓을 때,
각 원뿔의 부피를 구해 전체 부피를 계산하면,
총 얼마만큼의 꽃이나 흙이 들어갈지 미리 파악할 수 있습니다.
이처럼 실생활의 작은 호기심까지 원뿔 부피 공식으로 해결할 수 있습니다.
학교 과학 실험에서도 원뿔 부피 공식이 등장합니다.
예를 들어, 특정 물질의 부피를 측정할 때
원뿔형 용기에 담아 실험을 하는 경우가 있습니다.
이 때, 정확한 부피 계산을 위해
공식을 활용하면 실험 결과의 신뢰도가 높아집니다.
원뿔 부피 공식 요약
원뿔 부피 공식은 매우 간단하면서도,
수많은 실생활 상황에 유용하게 쓸 수 있습니다.
공식은 (1/3) × π × r² × h로,
밑면의 반지름과 원뿔의 높이만 알면 바로 계산이 가능합니다.
학교 수업에서 이 공식을 처음 배우는 학생이라면,
단순히 외우는 데 그치지 말고,
실제로 계산을 해보고,
여러 사례에 적용해 보는 연습이 필요합니다.
이 과정을 반복하다 보면,
자연스럽게 공식이 익숙해지고,
실생활에서 원뿔을 만날 때마다
부피 계산이 손쉬워질 것입니다.
원뿔 부피 공식은 수학의 기본 중 하나로,
학습 과정에서 반드시 익혀야 할 공식입니다.
반지름과 높이의 값만 알면,
누구나 쉽게 부피를 구할 수 있습니다.
이 공식을 통해 실생활의 다양한 문제를 해결할 수 있을 뿐만 아니라,
더 넓은 수학적 사고의 기초도 다질 수 있습니다.
원뿔 부피 공식을 익히고 싶다면,
반지름과 높이를 직접 재보고